Offline Incremental SCC
tags:algorithm
Outline
Hello, in this blog I’ll explain the algorithm from this Radewoosh blog. The linked blog is understandable and well-written (and honestly, this idea can be in summarized in one line as “dnc over timeline”) but it’s a bit informal and I feel like writing something, hence this blog.
Problem
We are going to learn to maintain information about SCCs in a directed graph when have a problem with the following general structure:
Given an initially empty digraph $G$, and a list of $m$ directed edges $E$ that are sequentially added to the graph, we need to answer queries of the following form: Find some information about SCCs in $G$ after the first $i$ edges are added
Some specific examples of queries would be:
-
Find the smallest $i$ such that $u$ and $v$ belong to the same SCC after the first $i$ edges are added.
-
Find the size of the SCC containing node $u$ after $i$ edges are added.
Note: As the title suggests, the idea described here is only applicable when we are allowed to process the queries offline.
Observations
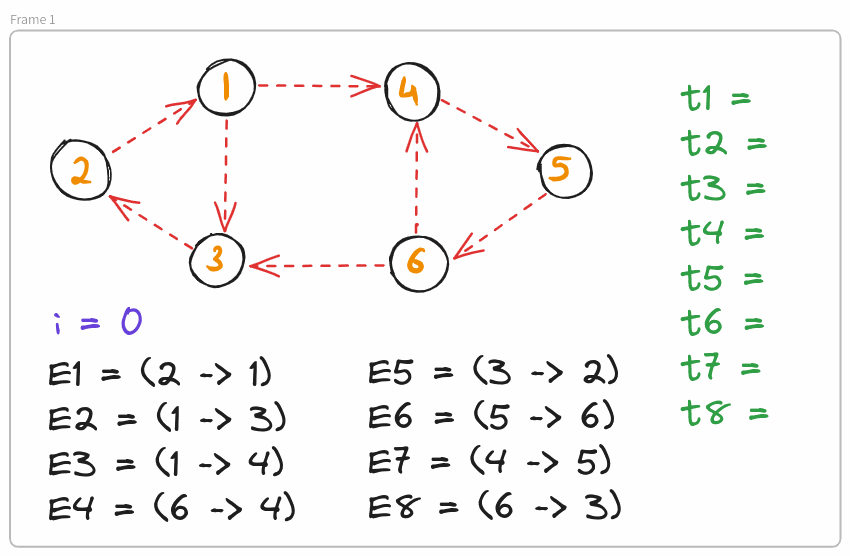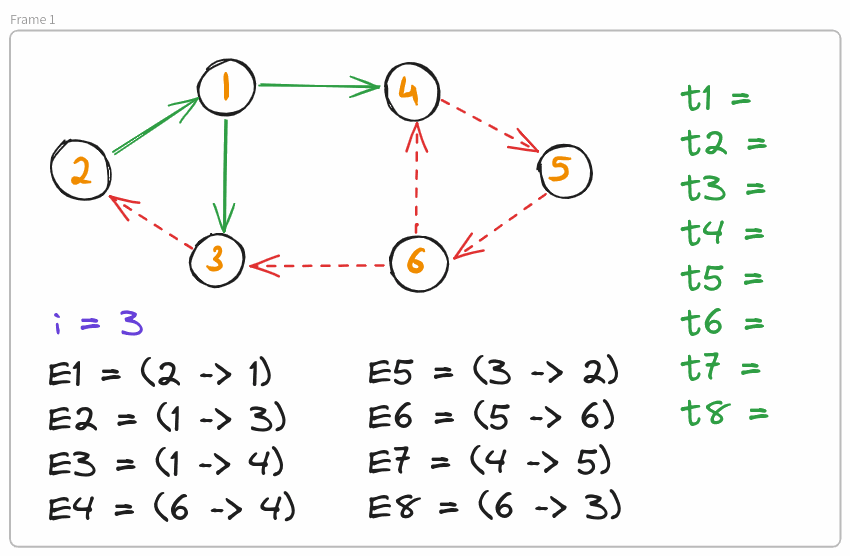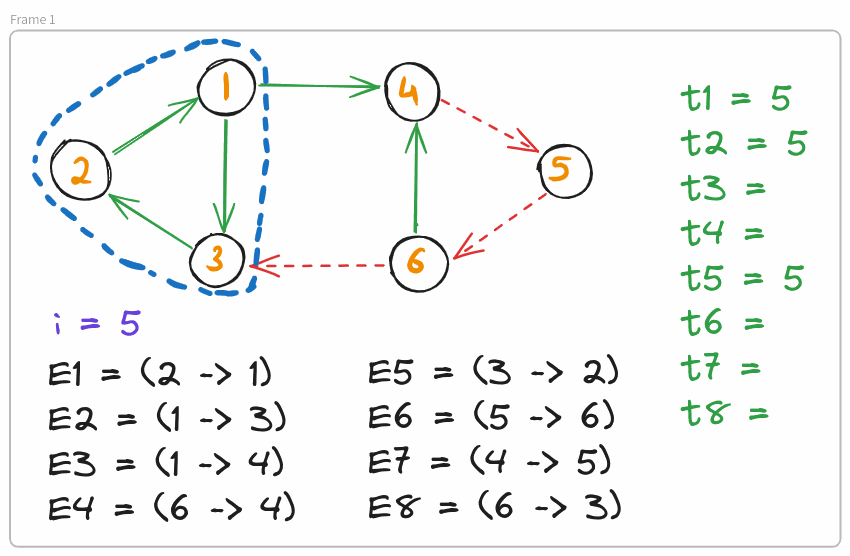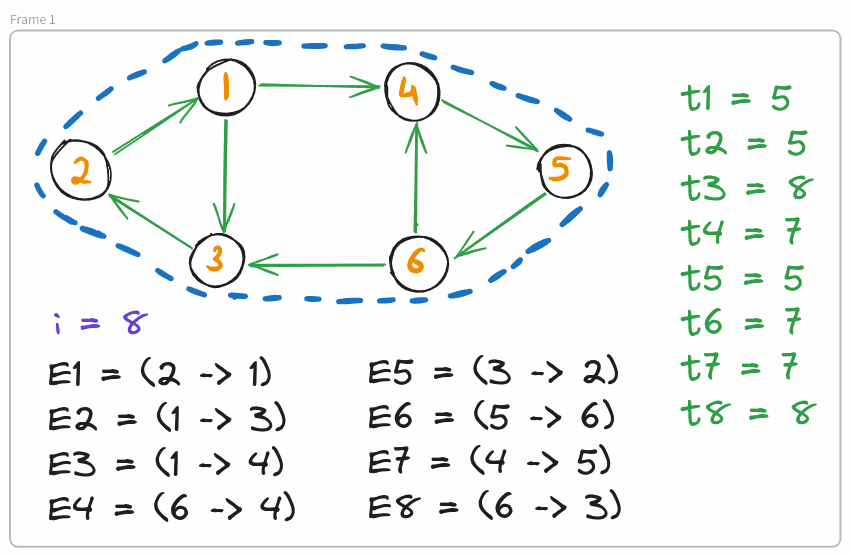
Notation: Define $S(u, i)$ to be the set of nodes in the SCC of node $u$ after the addition of the first $i$ edges to $G$
The entire algorithm is based around a trivial observation:
For every pair of nodes $(u, v)$ we have, $(S(u, j) \neq S(v, j)) \implies (S(u, k) \neq S(v, k)) \forall k \leq j$.
Therefore, for every edge $E_i = (u \rightarrow v)$, we define $t_i = \arg \min_j \left( S(u, j) = S(v, j) \right)$ (and trivially infinite if they are never equal). One can observe that the presence of $E_i$ in $G$ doesn’t affect the structure of any SCC until the the first $t_i$ edges are added.

Algorithm
Pre-Processing
We will be doing DnC over the timeline of addition of edges (ie, $[1, m]$) with a recursive function of the form $f(l, r, \text{edge list})$. For every call $f(l, r, \text{edge list})$, our $\text{edge list}$ will contain all edges $E_i$ for which $l \leq t_i \leq r$.
Let us look at what we do in the first call, $f(1, m, \text{edge list})$ to understand what the generalized recursive call will be doing:
-
Define $\text{mid} = (1 + m)/2$. We add all edges $E_i : i \leq \text{mid}$ to our initially empty graph and find SCCs induced by these edges. This can be done in $O(x)$ time where $x$ is the number of edges.
-
Store information about SCCs/answer queries.
-
For every edge $E_i = (u \rightarrow v) : i \leq \text{mid}$, if $\text{SCC}_u = \text{SCC}_v$, then we can deduce that $t_i \leq (1 + n)/2$. Otherwise, $t_i > \text{mid}$. Separate these edges into two groups $\text{G}_1$ and $\text{G}_2$ respectively. Add all edges $E_i : i > \text{mid}$ to $\text{G}_2$.
-
Call $f(1, \text{mid} - 1, \text{G}_1)$.
-
Once we return from this call, compress all the SCCs induced by the addition of edges in $\text{G}_1$.
-
Call $f(\text{mid} + 1, m, \text{G}_2)$. **Remember, this call must operate on the compressed graph.
Notice that when we execute $f(l, r, \text{edge list})$, it is essential that we perform the computation within it (finding SCCs induced by $\text{edge list}$, checking if endpoints of edges belong to the same SCC, etc.) upon the compressed graph induced by all edges $E_i : t_i < l$. This can be done easily by maintaining a global graph $G$, and performing compressions introduced by $\text{edge list}$ of $f(l, r, \text{edge list})$ when we return from this function (therefore, step $5$ will actually be performed by $f(1, \text{mid} - 1, \text{G}_1)$ and the calls in its subtree before they return).
The pseudo code for our algorithm takes the following form:
create an empty graph G with n nodes
def f(l, r, edge list):
mid = (l + r)/2
initialize SCC structure from G
for every edge E[i] = (u -> v) in edge list:
if(i <= mid)
add (u -> v) to SCC structure
compute SCCs
problem specific stuff (storing info/answering queries)
initialize empty edge lists G1 and G2
for every edge E[i] = (u -> v) in edge list:
if(i <= mid):
if(SCC[u] = SCC[v])
add E[i] to G1
else
add E[i] to G2
else
add E[i] to G2
f(l, mid - 1, G1)
f(mid + 1, r, G2)
for every SCC induced by G1:
compress SCC into a single node in G
enddef
f(1, m, edge list)
Answering Queries
This is quite problem-dependent. I have only seen a couple of problems which use this idea so I will just describe two ways of answering queries that I know of:
Queries based on number of edges added
These queries are of the form:
Find some information about the SCCs of a graph after $i$ edges are added.
Such queries can be answered by maintaining SCCs using DSU/Small-to-Large merging/(some other ds) as we go through the recursion in a way such that after performing the computation for $f(l, r, \text{edge list})$, all information about SCCs after adding the first $(l + r)/2$ edges will be queryable from our DS. We then answer all queries with $i = (l + r)/2$.
Note: This is possible because if the SCC compression for $f(l_1, r_1, \text{edge list}_1)$ is done before the SCC compression for $f(l_2, r_2, \text{edge list}_2)$, then we have either $(l_1 \leq l_2 \text{ and } r_1 \leq r_2)$ or $(l_2 \leq l_1 \text{ and } r_1 \leq r_2)$. Therefore, SCCs only expand(unite) as we recurse through the calls.
Queries based on nodes
This is a somewhat non-trivial technique, which can be used to answer queries like:
Find the smallest $i$ such that nodes $u$ and $v$ belong to the same SCC after the first $i$ edges are added to $G$
We solve it in the following way:
-
We maintain an initially empty undirected weighted graph $U$.
-
At every call $f(l, r, \text{edge list})$, for every edge $E_i = (u \rightarrow v) \in \text{G}1$, we add an edge $(u, v)$ with weight $(l + r)/2$ to $U$.
-
Finally, $U$ contains $O(m\log_2{m})$ edges, with weights $\leq m$.
-
To answer a query for a pair of nodes $(u, v)$, one can observe that the problem is equivalent to finding the minimized maximum weight edge on any path between $u$ and $v$ in $U$. This can be done by constructing the MST of $U$ and answering path maximum queries.
Note: Since all edges in $U$ have weight $\leq m$, we can avoid sorting its edge list and simply iterate over edge weights (in kruskals) to find the MST and get rid of a log factor, allowing construction of the MST in $O(m\log_2{m})$.
Complexity Analysis
Since we split apart $\text{edge list}$ into two disjoint groups $\text{G}1$ and $\text{G}2$ in every call $f(l, r, \text{edge list})$, this ensures that every edge occurs exactly once on every level of the recursion. For every call $f(l, r, \text{edge list})$, we perform a $O(\vert \text{edge list} \vert)$ computation. So on every level, we perform a $O(\sum_{f(l, r, \text{edge list})}(\vert \text{edge list} \vert)) = O(m)$ computation. There are $\log_2(m)$ levels of the recursion, so our pre-processing algorithm works in $O(m \log_2{m})$.
The time taken for answering queries is problem dependent.